Electron-positron annihilation¶
Calculation of positron lifetime and momentum distribution in silicon¶
This tutorial aims at showing how to perform Two-Component Density-Functional Theory (TCDFT) calculations in the PAW framework to obtain the following physical properties:
- the positron lifetime in the perfect material,
- the lifetime of a positron localized in a vacancy,
- the electron-positron momentum distribution.
For the description of the implementation of TCDFT in ABINIT see [Wiktor2015].
The user should be familiar with the four basic tutorials of ABINIT and the first PAW tutorial.
This tutorial should take about 2 hours.
Note
Supposing you made your own install of ABINIT, the input files to run the examples are in the ~abinit/tests/ directory where ~abinit is the absolute path of the abinit top-level directory. If you have NOT made your own install, ask your system administrator where to find the package, especially the executable and test files.
To execute the tutorials, create a working directory (Work*) and
copy there the input files and the files file of the lesson. This will be explicitly mentioned in the first lessons,
that will tell you more about the files file (see also section 1.1).
The files file ending with _x (e.g. tbase1_x.files) must be edited every time you start to use a new input file.
Most of the tutorials do not rely on parallelism (except specific tutorials on parallelism). However you can run most of the tutorial examples in parallel, see the topic on parallelism.
In case you work on your own PC or workstation, to make things easier, we suggest you define some handy environment variables by executing the following lines in the terminal:
export ABI_HOME=Replace_with_the_absolute_path_to_the_abinit_top_level_dir export PATH=$ABI_HOME/src/98_main/:$PATH export ABI_TESTS=$ABI_HOME/tests/ export ABI_PSPDIR=$ABI_TESTS/Psps_for_tests/ # Pseudopotentials used in examples.
Examples in this tutorial use these shell variables: copy and paste the code snippets into the terminal (remember to set ABI_HOME first!). The ‘export PATH’ line adds the directory containing the executables to your PATH so that you can invoke the code by simply typing abinit in the terminal instead of providing the absolute path.
Computing the positron lifetime in Si lattice¶
Before beginning, you might consider to work in a different subdirectory as for the other tutorials. Why not Work_positron?
cd $ABI_TESTS/tutorial/Input mkdir Work_positron cd Work_positron cp ../tpositron_x.files . # You will need to edit this file. cp ../tpositron_1.in .
The tutorial begins with a calculation of the positron lifetime in a silicon lattice. In a perfect material the positron is delocalized. We can assume that its density approaches zero and that it cannot affect the electron density. We will perform a calculation in only two steps:
- Calculation of the ground-state electron density without the positron.
- Calculation of the ground-state positron density in the presence of the electron density from step 1.
The two densities are used to calculate the positron lifetime, which is proportional to the inverse of the overlap of the electron and positron densities. This 2-step calculation, considering the zero-positron density limit, corresponds to the conventional scheme (CONV).
In the tpositron_1.in file, you will find two datasets.
################################################################# # Input file for the positron tutorial # # Positron lifetime calculation within PAW # # # # Si, 2 atoms in the box # ################################################################# # Datasets definition ndtset 2 positron1 0 ! Dataset 1 is a simple electronic GS calculation positron2 1 ! Dataset 2 is a positronic GS calculation getden2 1 ! in presence of the previous electronic density kptopt2 0 ! Use only k=gamma point ixcpositron2 1 ! We are using the Boronski and Nieminen parametrization # Common input parameters ! Unit cell acell 3*5.43 angstrom rprim 0.0 0.5 0.5 0.5 0.0 0.5 0.5 0.5 0.0 natom 2 ntypat 1 typat 2*1 znucl 14 xred 0.0 0.0 0.0 0.25 0.25 0.25 ! K-points and occupations kptopt 1 ngkpt 4 4 4 nshiftk 1 shiftk 0.0 0.0 0.0 occopt 1 nband 6 posocc2 1 ! Occupation number for the positron (should be set <1 for bulk calculation with a small cell). ! Here the zero positron density limit is used, so results do not depend on posocc. ! Convergence parameters ecut 8. pawecutdg 15. iscf 17 nstep 50 tolvrs 1.d-8 ! Miscelaneous prtwf 0 prteig 0 ! To save disk space optforces 0 optstress 0 ! Not relevant here #%%<BEGIN TEST_INFO> #%% [setup] #%% executable = abinit #%% [files] #%% files_to_test = #%% tpositron_1.out, tolnlines= 0, tolabs= 0.0, tolrel= 0.0, fld_options= -easy #%% psp_files = Si.LDA-PW-paw.abinit #%% [paral_info] #%% max_nprocs = 10 #%% [extra_info] #%% authors = J. Wiktor #%% keywords = POSITRON,PAW #%% description = First step of the tutorial on electron-positron annihilation #%%<END TEST_INFO>
The first dataset is a standard ground-state calculation. The second one introduces a positron into the system. You can see that in this case we set:
positron2 1 ! Dataset 2 is a positronic GS calculation getden2 1 ! in presence of the previous electronic density kptopt2 0 ! Use only k=gamma point ixcpositron2 1 ! We are using the Boronski and Nieminen parametrization
Here we set positron=1, which corresponds to a positronic ground-state calculation, considering that the electrons are not perturbed by the presence of the positron (zero-positron density limit). The electron density is read from the file resulting from dataset 1. As we consider the positron to be completely delocalized, we only consider the Γ point in the Brillouin zone. The keyword ixcpositron selects the electron- positron correlation functional and enhancement factor. In this calculation we use the functional parametrized by Boronski and Nieminen [Boronski1986], using the data provided by Arponen and Pajanne [Arponen1979].
We can now run the calculation. In the directory
~abinit/tests/tutorial/Input/Work_positron, copy the files
~abinit/tests/tutorial/Input/tpositron_x.files and tpositron_1.in.
Then, issue:
abinit < tpositron_x.files > log 2> err &
This calculation should only take a few seconds.
You can look at the tpositron_1.out file. We find the positron lifetime calculated in the RPA limit:
########## Lifetime computation 2 # Zero-positron density limit of Arponen and Pajanne provided by Boronski & Nieminen Ref.: Boronski and R.M. Nieminen, Phys. Rev. B 34, 3820 (1986) # Enhancement factor of Boronski & Nieminen IN THE RPA LIMIT Ref.: Boronski and R.M. Nieminen, Phys. Rev. B 34, 3820 (1986) Positron lifetime (ps) = 2.22891945E+02
The lifetime of 223 ps agrees well with the value of 225 ps calculated with the same number of valence electrons in [Wiktor2015] and with the experimental value of about 219 ps [Panda1997].
Important
If we had not used the “zero positron density limit” approximation (using, for example, another value of ixcpositron), we would theoretically have needed a box of infinite size for the positron to completely delocalise itself in the crystal. This can be avoided by the use of the posocc input parameter. Numerically, it is equivalent to calculate the density of 1 positron in a box of size N and that of x positron in a box of size N * x. Thus, we can calculate the lifetime of a positron in a primitive cell by setting posocc to a small value (0.0001 …). This value must obviously be tested…
Computing the positron lifetime in a Si monovacancy¶
We will now perform a positron lifetime calculation for a monovacancy in silicon in the conventional scheme (which we applied to the perfect lattice previously). Note that when the positron localizes inside a vacancy, the zero- positron density limit does not apply anymore. However, in some cases, the conventional scheme proved to yield results in agreement with experiments.
For the purpose of this tutorial, we generate a defect in a cell containing only 16 atoms. This supercell is too small to get converged results, but the calculation is relatively fast.
################################################################# # Input file for the positron tutorial # # Positron lifetime calculation within PAW # # # # Si monovacancy, "conventional" scheme # ################################################################# # Datasets definition ndtset 2 positron1 0 ! Dataset 1 is a simple electronic GS calculation positron2 1 ! Dataset 2 is a positronic GS calculation getden2 1 ! in presence of the previous electronic density kptopt2 0 ! Use only k=gamma point ixcpositron2 1 ! We are using the Boronski and Nieminen parametrization # Common input parameters ! Unit cell acell 3*5.43 angstrom rprim 0.0 1.0 1.0 1.0 0.0 1.0 1.0 1.0 0.0 chkprim 0 natom 15 ntypat 1 typat 15*1 znucl 14 xred 0.0 0.0 0.0 0.0 0.0 0.5 0.0 0.5 0.0 0.5 0.0 0.0 0.0 0.5 0.5 0.5 0.0 0.5 0.5 0.5 0.0 0.5 0.5 0.5 0.125 0.125 0.125 0.125 0.125 0.625 0.125 0.625 0.125 0.625 0.125 0.125 0.125 0.625 0.625 0.625 0.125 0.625 0.625 0.625 0.125 ! 0.625 0.625 0.625 ! We remove one Si atom ! K-points and occupations kptopt 1 ngkpt 2 2 2 nshiftk 1 shiftk 0.0 0.0 0.0 occopt 1 nband 36 posocc2 1.0 ! Occupation number for the positron (should be set <1 for bulk calculation with a small cell). ! Here the zero positron density limit is used, so results do not depend on posocc. ! Convergence parameters ecut 8. pawecutdg 15. iscf 17 nstep 50 tolvrs 1.d-8 ! Miscelaneous prtwf 0 prteig 0 ! To save disk space optforces 0 optstress 0 ! Not relevant here #%%<BEGIN TEST_INFO> #%% [setup] #%% executable = abinit #%% [files] #%% files_to_test = #%% tpositron_2.out, tolnlines= 0, tolabs= 0.0, tolrel= 0.0, fld_options= -easy #%% psp_files = Si.LDA-PW-paw.abinit #%% [paral_info] #%% max_nprocs = 10 #%% [extra_info] #%% authors = J. Wiktor #%% keywords = POSITRON,PAW #%% description = Second step of the tutorial on electron-positron annihilation #%%<END TEST_INFO>
You can now, issue (after having replaced tpositron_1 by tpositron_2 in the tpositron_x.files file):
abinit < tpositron_x.files > log 2> err &
Once the calculation is finished, look at the tpositron_2.out file. Again, we look at the reported lifetime:
########## Lifetime computation 2 # Zero-positron density limit of Arponen and Pajanne provided by Boronski & Nieminen Ref.: Boronski and R.M. Nieminen, Phys. Rev. B 34, 3820 (1986) # Enhancement factor of Boronski & Nieminen IN THE RPA LIMIT Ref.: Boronski and R.M. Nieminen, Phys. Rev. B 34, 3820 (1986) Positron lifetime (ps) = 2.46936401E+02
We observe that when the positron localizes inside the vacancy, its lifetime increases from 223 to 247 ps. This is because now the majority of the positron density is localized in the vacancy region, where the electron density is small. The overlap of the electron and positron densities is reduced, and the lifetime increased.
In the Work_positron directory, you will also find a tpositron_2o_DS2_DEN_POSITRON file, containing the positron density. Visualizing this file (using e.g. cut3d and XcrysDen or VMD ) you can see that the positron is localized inside the vacancy. You can see below how the positron (in red, isodensity at 30% of the maximum density) localized the silicon monovacancy looks like:
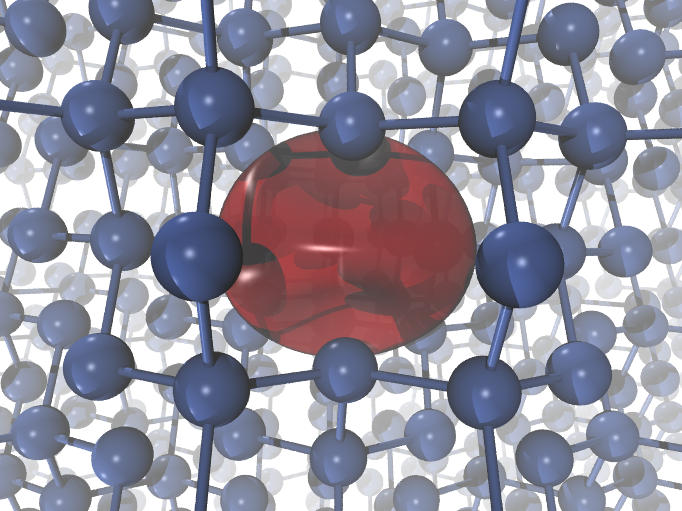
Performing a self-consistent electron-positron calculation for a Si vacancy¶
We will now perform a self-consistent calculation of the positron and electron densities. As this calculation will take a few minutes, you can already issue (putting tpositron_3.in in tpositron_x.files):
abinit < tpositron_x.files > log 2> err &
################################################################# # Input file for the positron tutorial # # Positron lifetime calculation within PAW # # # # Si monovacancy, self-consistent scheme # ################################################################# # Self-consistent positron lifetime calculation positron -10 ! We perform automatic calculation of electrons and positron densities in the two-component DFT context postoldfe 1d-5 ! We will repeat the electon and positron steps until the energy difference is lower than 1d-5 posnstep 20 ! Maximum number of electon and positron steps ixcpositron 1 ! We are using the Boronski and Nieminen parametrization # Common input parameters ! Unit cell acell 3*5.43 angstrom rprim 0.0 1.0 1.0 1.0 0.0 1.0 1.0 1.0 0.0 chkprim 0 natom 15 ntypat 1 typat 15*1 znucl 14 xred 0.0 0.0 0.0 0.0 0.0 0.5 0.0 0.5 0.0 0.5 0.0 0.0 0.0 0.5 0.5 0.5 0.0 0.5 0.5 0.5 0.0 0.5 0.5 0.5 0.125 0.125 0.125 0.125 0.125 0.625 0.125 0.625 0.125 0.625 0.125 0.125 0.125 0.625 0.625 0.625 0.125 0.625 0.625 0.625 0.125 ! 0.625 0.625 0.625 ! We remove one Si atom ! K-points and occupations kptopt 1 ngkpt 2 2 2 nshiftk 1 shiftk 0.0 0.0 0.0 occopt 1 nband 36 posocc 1.0 ! Occupation number for the positron (we have one positron in the cell). ! Convergence parameters ecut 8. pawecutdg 15. iscf 17 nstep 500 ! We increase nstep toldfe 1.d-8 ! Miscelaneous prtwf 0 prteig 0 ! To save disk space optforces 0 optstress 0 ! Not relevant here #%%<BEGIN TEST_INFO> #%% [setup] #%% executable = abinit #%% [files] #%% files_to_test = #%% tpositron_3.out, tolnlines= 30, tolabs= 9.0e-4, tolrel= 4.0e-1, fld_options= -easy #%% psp_files = Si.LDA-PW-paw.abinit #%% [paral_info] #%% max_nprocs = 10 #%% [extra_info] #%% authors = J. Wiktor #%% keywords = POSITRON,PAW #%% description = Third step of the tutorial on electron-positron annihilation #%%<END TEST_INFO>
This calculation is significantly longer than the previous one, because the electron and positron steps will be repeated until the convergence criterion is reached.
In tpositron_3.in we only have one dataset and we set positron = -10 to perform an automatic calculation of electrons and positron densities. The convergence is controlled by postoldfe = 1d-5. This means that we will repeat the electron and positron steps until the energy difference between them is lower than 1d-5 Ha. This value should always be larger than toldfe. In this calculation we still use ixcpositron = 1, which means that we are using the GGGC scheme (see [Gilgien1994] and [Wiktor2015]
Once the calculation is finished, look at the positron lifetime in tpositron_3.out.
########## Lifetime computation 2 # Zero-positron density limit of Arponen and Pajanne provided by Boronski & Nieminen Ref.: Boronski and R.M. Nieminen, Phys. Rev. B 34, 3820 (1986) # Enhancement factor of Boronski & Nieminen IN THE RPA LIMIT Ref.: Boronski and R.M. Nieminen, Phys. Rev. B 34, 3820 (1986) Positron lifetime (ps) = 2.55617112E+02
Including the self-consistency increases the positron lifetime, because its localization inside the vacancy becomes stronger when the positron and the electron densities are allowed to relax.
Relaxing the vacancy according to forces due to electrons and the positron¶
In addition to the self-consistency, the lifetime of a positron inside a vacancy can be strongly affected by the relaxation of the atoms due to the forces coming from both the electrons and the positron. You can already start the relaxation of the vacancy by issuing:
abinit < tpositron_4.files > log 2> err &
Important
Don’t forget to put tpositron_4.in in tpositron_x.files.
In this calculation we switched on the atomic relaxation by setting ionmov = 2. We need to calculate forces to be able to move the atoms, so we set optforces = 1. In the provided tpositron_4.in file, we only perform 4 relaxation steps (ntime = 4) to save time, but more steps would be needed to converge the positron lifetime.
################################################################# # Input file for the positron tutorial # # Positron lifetime calculation within PAW # # # # Si monovacancy, self-consistent scheme # ################################################################# # Self-consistent positron lifetime calculation positron -10 ! We perform automatic calculation of electrons and positron densities in the two-component DFT context postoldfe 1d-5 ! We will repeat the electon and positron steps until the energy difference is lower than 1d-5 posnstep 20 ! Maximum number of electon and positron steps ixcpositron 1 ! We are using the Boronski and Nieminen parametrization # Common input parameters ! Unit cell acell 3*5.43 angstrom rprim 0.0 1.0 1.0 1.0 0.0 1.0 1.0 1.0 0.0 chkprim 0 natom 15 ntypat 1 typat 15*1 znucl 14 xred 0.0 0.0 0.0 0.0 0.0 0.5 0.0 0.5 0.0 0.5 0.0 0.0 0.0 0.5 0.5 0.5 0.0 0.5 0.5 0.5 0.0 0.5 0.5 0.5 0.125 0.125 0.125 0.125 0.125 0.625 0.125 0.625 0.125 0.625 0.125 0.125 0.125 0.625 0.625 0.625 0.125 0.625 0.625 0.625 0.125 ! 0.625 0.625 0.625 ! We remove one Si atom ! K-points and occupations kptopt 1 ngkpt 2 2 2 nshiftk 1 shiftk 0.0 0.0 0.0 occopt 1 nband 36 posocc 1.0 ! Occupation number for the positron (we have one positron in the cell). ! Convergence parameters ecut 8. pawecutdg 15. iscf 17 nstep 500 ! We increase nstep toldfe 1.d-8 ! Miscelaneous prtwf 0 prteig 0 ! To save disk space optforces 0 optstress 0 ! Not relevant here #%%<BEGIN TEST_INFO> #%% [setup] #%% executable = abinit #%% [files] #%% files_to_test = #%% tpositron_3.out, tolnlines= 30, tolabs= 9.0e-4, tolrel= 4.0e-1, fld_options= -easy #%% psp_files = Si.LDA-PW-paw.abinit #%% [paral_info] #%% max_nprocs = 10 #%% [extra_info] #%% authors = J. Wiktor #%% keywords = POSITRON,PAW #%% description = Third step of the tutorial on electron-positron annihilation #%%<END TEST_INFO>
Look at the positron lifetime in the RPA limit after each ionic step:
Positron lifetime (ps) = 2.55617112E+02 Positron lifetime (ps) = 2.56981105E+02 Positron lifetime (ps) = 2.81986785E+02 Positron lifetime (ps) = 2.82826327E+02
As the vacancy relaxes outwards, the positron lifetime increases. 4 steps were not enough to relax the defect completely, as the lifetime still changes. Indeed, setting ntime to 10 delivers:
Positron lifetime (ps) = 2.55617112E+02 Positron lifetime (ps) = 2.56981106E+02 Positron lifetime (ps) = 2.81986782E+02 Positron lifetime (ps) = 2.82826326E+02 Positron lifetime (ps) = 2.86660064E+02 Positron lifetime (ps) = 2.87040831E+02 Positron lifetime (ps) = 2.87284438E+02 Positron lifetime (ps) = 2.87360829E+02 Positron lifetime (ps) = 2.87302206E+02
Although the results at ionic steps 3 and 4 differ from each other by less than one percent, they differ by more from the final result. The one percent convergence is only reached at ionic step 5 and after.
Also, remember that the 16-atom supercell is not large enough to get converged results. In Table IV of [Wiktor2015] you can see converged results of the positron lifetime of Si monovacancy within various methods.
Computing the electron-positron momentum distribution (Doppler spectrum) of a Si lattice¶
In the last part of the tutorial we will calculate the electron-positron momentum distribution (Doppler spectrum) of a silicon lattice in the conventional scheme. This type of calculation is much more time and memory consuming than the lifetime calculation, as it is using the electron and positron wavefunctions (not only densities).
You can already issue (putting tpositron_5.in in tpositron_x.files):
abinit < tpositron_5.files > log 2> err &
Now take a look at the input file tpositron_5.in.
################################################################# # Input file for the positron tutorial # # Doppler spectrum calculation within PAW # # # # Si, 2 atoms in the box # ################################################################# positron -10 ! Electron/positron GS calculation ! Automatic electron-positron loop has to be switched on in Doppler calculations ! to have both electron and positron wavefunctions in memory posnstep 2 ! We simulate a delocalized positron, so we only perform two steps of electon-positron calculations. ! It means that the electronic wavefunction is not affected by the positron. posdoppler 1 ! Activation of Doppler broadening calculation ixcpositron 1 ! We are using the Boronski and Nieminen parametrization # Common input parameters ! Unit cell acell 3*5.43 angstrom rprim 0.0 0.5 0.5 0.5 0.0 0.5 0.5 0.5 0.0 natom 2 ntypat 1 typat 2*1 znucl 14 xred 0.0 0.0 0.0 0.25 0.25 0.25 ! K-points and occupations ! In Doppler calculation we need to have a uniform ! grid in the momentum space. Symmetries are not used, ! so the full grid needs to be specified. kptopt 0 istwfk *1 nkpt 8 ! This corresponds to a 2x2x2 grid, denser grids may be needed to get converged spectra kpt 0 0 0 0 0 0.5 0 0.5 0 0.5 0 0 0 0.5 0.5 0.5 0 0.5 0.5 0.5 0 0.5 0.5 0.5 occopt 1 nband 6 posocc 1.0 ! Occupation number for the positron (should be set <1 for bulk calculation with a small cell). ! Here the zero positron density limit is used, so results do not depend on posocc. ! Convergence parameters ecut 8. pawecutdg 15. iscf 17 nstep 50 tolvrs 1.d-8 ! Miscelaneous prtwf 0 prteig 0 ! To save disk space optforces 0 optstress 0 ! Not relevant here #%%<BEGIN TEST_INFO> #%% [setup] #%% executable = abinit #%% [files] #%% files_to_test = #%% tpositron_5.out, tolnlines= 5, tolabs= 2.6e-2, tolrel= 3.8e-2, fld_options= -easy #%% psp_files = Si.LDA-PW-paw.abinit #%% [paral_info] #%% max_nprocs = 10 #%% [extra_info] #%% authors = J. Wiktor #%% keywords = POSITRON,PAW #%% description = Fifth step of the tutorial on electron-positron annihilation #%%<END TEST_INFO>
The momentum distribution calculation is activated by posdoppler = 1. You can also notice that instead of having two datasets as in the first part of this tutorial, we now use the automatic electron-positron loop and set posnstep = 2. This is done because we need to have the full electron and positron wavefunctions in memory, which is only the case when positron <= -10. Additionally, the momentum distribution calculations require using a full k-point grid. In the input file we set:
kptopt 0 istwfk *1 nkpt 8 # This corresponds to a 2x2x2 grid, denser grids may be needed to get converged spectra kpt 0 0 0 0 0 0.5 0 0.5 0 0.5 0 0 0 0.5 0.5 0.5 0 0.5 0.5 0.5 0 0.5 0.5 0.5
This grid is used in both electron and positron calculations, but only the positron wavefunction at the first point is taken in the momentum distribution calculation, so the \Gamma point should always be given first.
In the calculation of the momentum distribution, we need to include both core
and valence electrons. The wavefunctions of the core electrons are read from a
file (one per atom type), which needs to be provided. This core WF file should
be named <psp_file_name>.corewf (where <psp_file_name> is the name of the
pseudo-potential (or PAW) file) or corewf.abinit<ityp> (where <ityp> is the
index of the atom type). Core WF files can be obtained with the atompaw tool
(see the tutorial on generating PAW datasets (PAW2) ) by the use of the
prtcorewf keyword. You will find the core wavefunction file used in this calculation in
$ABI_PSPDIR/Si.LDA-PW-paw.abinit.corewf.
Once the calculation is complete, you can find a tpositron_5o_DOPPLER file
containing the momentum distribution on the FFT grid. You can use the
~abinit/scripts/post_processing/posdopspectra.F90 tool to generate 1D
projections (Doppler spectra) in (001), (011) and (111) directions and to
calculate the low- and high-momentum contributions to the
momentum distribution (so called S and W parameters, see [Wiktor2015]).
Studying the effect of the PAW dataset completeness¶
The positron lifetime and momentum distribution calculations within the PAW method are very sensitive to the number of valence electrons in the PAW dataset. It is due to the fact that it is not easy to describe the positron wavefunction, tending to zero at the nucleus, using the electron atomic orbitals. The PAW basis set in this case needs to be more complete than only for describing the electron wavefunctions.
The simplest way to make the PAW
dataset more complete is to include semicore electrons. It is also possible to
add the partial waves corresponding to the semicore electrons in the basis
used only for the positron wave function description, while keeping the
initial number of valence electrons (as done in [Wiktor2015]). However, this second method is less straightforward.
The previous calculations were done with only 4 valence electrons (3s and 3p).
We will now see what happens if we include the 2s and 2p states in the PAW dataset.
In tpositron_12el_x.files we have replaced the Si.LDA-PW-paw.abinit
dataset with Si.12el.LDA-PW-paw.abinit. We can now rerun the lifetime calculation:
abinit < tpositron_12el_x.files > log 2> err
We now find the positron lifetime calculated in the RPA limit:
########## Lifetime computation 2 # Zero-positron density limit of Arponen and Pajanne provided by Boronski & Nieminen Ref.: Boronski and R.M. Nieminen, Phys. Rev. B 34, 3820 (1986) # Enhancement factor of Boronski & Nieminen IN THE RPA LIMIT Ref.: Boronski and R.M. Nieminen, Phys. Rev. B 34, 3820 (1986) Positron lifetime (ps) = 2.11481560E+02
This value is significantly lower than 223 ps achieved with 4 valence electrons in the first step. It is, therefore, very important to always test the PAW dataset completeness for positron calculations.
The PAW dataset completeness is even more important in the Doppler spectra calculations. We will now recalculate the momentum distribution including 12 valence electrons (using tpositron_7.in in tpositron_12el_x.files):
abinit < tpositron_12el_x.files > log 2> err
Before processing the new tpositron_7o_DOPPLER file, you should copy files
rho_001, rho_011, rho_111 from the fifth step to for instance si4el_001, si4el_011 and si4el_111.
By plotting the Doppler spectra in the (001) direction calculated with 4 and
12 valence electrons, you should obtain a figure like this:
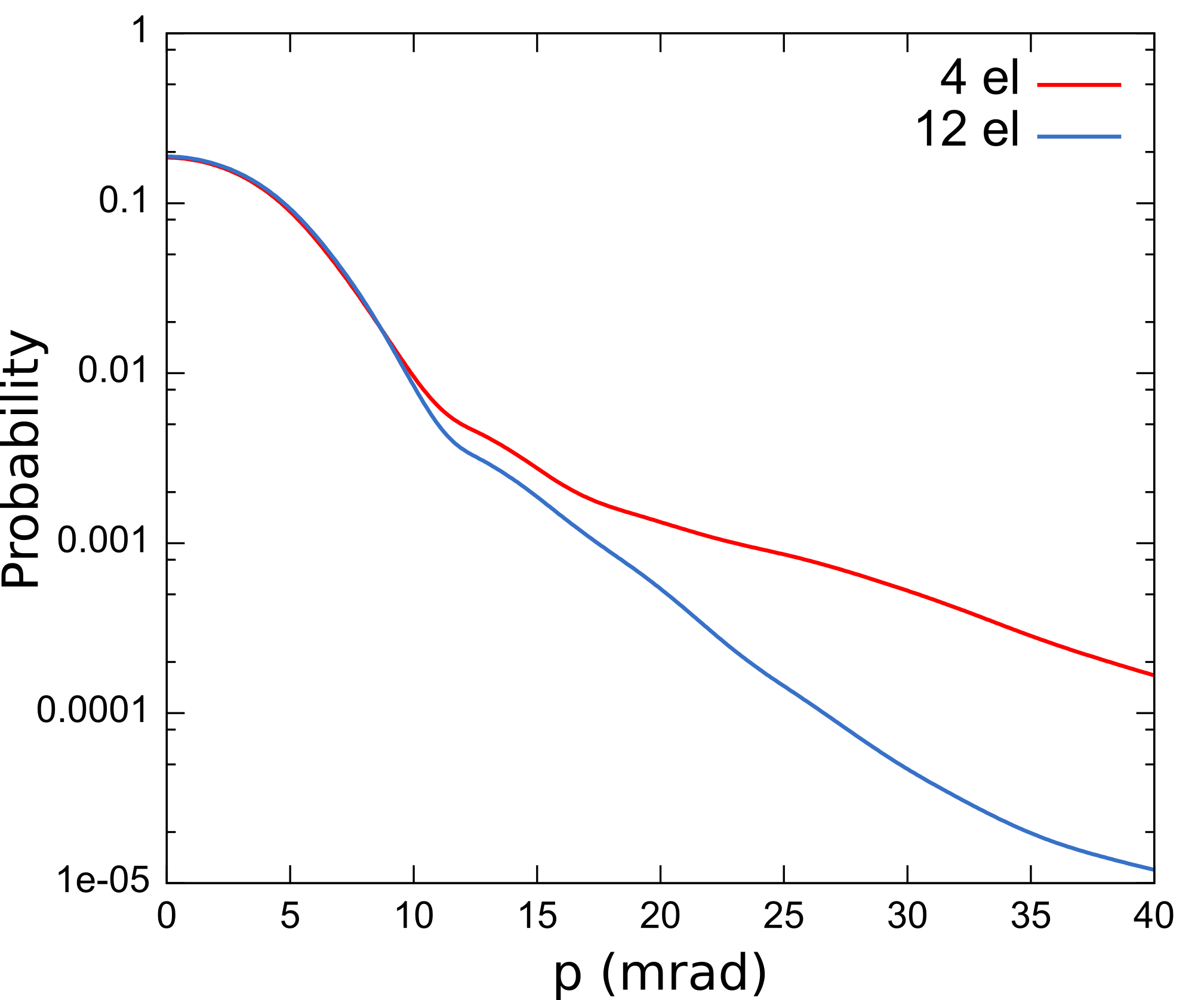
The dataset with 4 valence electrons is not complete enough to describe the
positron wavefunction around the nucleus. This is reflected in the
unphysically high probability at high momenta in the spectrum.
Further explanation of the influence of the PAW dataset on the Doppler spectra can be found in [Wiktor2015]. In case you need to generate your own dataset for momentum distribution calculations, you can follow the tutorial on generating PAW datasets (PAW2).